Numerické metody

Note

Iterativní metody pro řešení nelineárních rovnic (Newtonova metoda a její modifikace). Přímé metody pro řešení systému lineárních rovnic (Gaussova eliminace, Jacobi, Gauss-Seidel, relaxační metody). Numerická diferenciace, diferenciační schémata.
MA018

• Numerická analýza / numerical analysis
  Oblast matematiky / informatiky zabývající se tvorbou numerických metod a algoritmů, které řeší problémy matematické analýzy (např. derivace, integrály a podobný symbolický balast) pomocí numerické aproximace. ¹

  Je výhodná v situacích, kdy problém nelze řešit analyticky nebo je to příliš složité a není to (výpočetní) čas.

• Notace chyb

  • $x$ je přesná hodnota,
  • $\tilde{x}$ je aproximace $x$,
  • $x - \tilde{x}$ je absolutní chyba $\tilde{x}$,
  • $\lvert x - \tilde{x} \rvert \leq \alpha$ je odhad absolutní chyby,
  • $\frac{x - \tilde{x}}{x}$ je relativní chyba,
  • $\left\lvert \frac{x - \tilde{x}}{x} \right\rvert \leq \alpha$ je odhad relativní chyby.

• Numerická stabilita
  Schopnost numerické metody zpracovat chyby vstupních dat a výpočetních operací.

  Desetinná čísla jsou v počítačích nevyhnutelně reprezentována nepřesně. Numericky stabilní metody jsou takové, které tyto nepřesnosti nezhoršují. ²

• Řád metody / order of accuracy / order of approximation
  Hodnota reprezentující, jak rychle metoda konverguje k výsledku, resp. jak přesný je její odhad.

  Numerická metoda obvykle konverguje snižováním nějakého kroku $h$. Pokud ho lze zvolit libovolně malý, a lze-li prohlásit, že pro chybu aproximace $E$ platí: ^{3 4 5}

  $$\begin{aligned} E(h) &\leq C \cdot h^p \\ E(h) &\in \mathcal{O}(h^p) \end{aligned}$$

  kde $C$ je konstanta. Pak $p$ je řád metody.

Iterativní metody pro řešení nelineárních rovnic

• Root-finding problem
  Problém nalezení kořenů (root) funkce $f$. T.j. takových parametrů $x, ...$, kde funkce vrací 0: ⁶

  $$f(x, ...) = 0$$

• Iterative methods for root-finding problem
  Metody pro řešení root-finding problemu, které využívají iterativního přístupu. Tedy opakují nějaký výpočet a zpřesňují svůj odhad, dokud nedosáhnou požadované přesnosti. ^{7 6}

• Řád metody / rate of convergence
  Hodnota reprezentující, jak rychle metoda konverguje k výsledku. ³

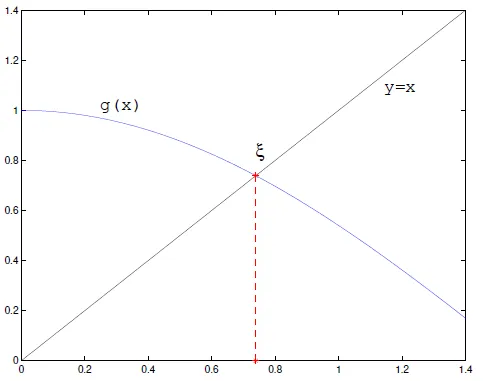
• Prostá iterační metoda / metoda pevného bodu / fixed-point iteration
  Používá se pro rovnice typu $x = g(x)$.

  1. Zvolíme počáteční odhad $x_0$.

  2. Opakujeme $x_{n+1} = g(x_n)$ dokud $\lvert x_{n+1} - x_n \rvert \leq \alpha$ (kde $\alpha$ je požadovaná přesnost).

     

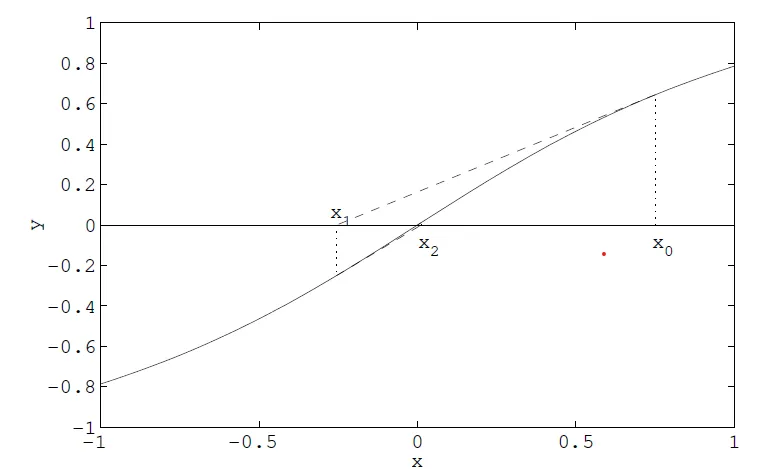
• Newtonova metoda / metoda tečen
  Používá k odhadu kořene funkce $f$ její tečnu v bodě $x_n$. Iterační funkce je:

  $$g(x_{k+1}) = x_k - \frac{f(x_k)}{f'(x_k)}$$

  1. Zvolíme počáteční odhad $x_0$.

  2. Další odhad je $x_{n+1} = g(x_n)$, tedy průsečík tečny fukce $f$ v bodě $x_n$ s osou $x$.

  3. Opakujeme 2. dokud nedosáhneme požadované přesnosti odhadu.

     

  Tip

  How to derive Newton approximation method:

  1. Start with Taylor $f(x)=\sum_{n=0}^{1} \frac{f_n(a)}{n!} \cdot (x-a)^n$
  2. Substitute $a = x_n$

  $f(x) \approx f(x_n) + f'(x_n)(x-x_n)$

  Now, we want to find $x_{n+1}$ such that $f(x) = f(x_{n+1}) = 0$.

  $$\begin{aligned} 0 \approx &\ f(x_n) + f'(x_n)(x_{n+1}-x_n) \\ 0 \approx &\ \frac{f(x_n)}{f'(x_n)} + x_{n+1} - x_n \\ x_{n+1} = &\ x_n - \frac{f(x_n)}{f'(x_n)} \end{aligned}$$

• Metoda sečen / secant method
  Používá k odhadu kořene funkce $f$ sečny, resp. finite difference, které aproximují derivaci funkce $f$. Díky tomu není potřeba znát derivaci funkce $f$. Iterační funkce je: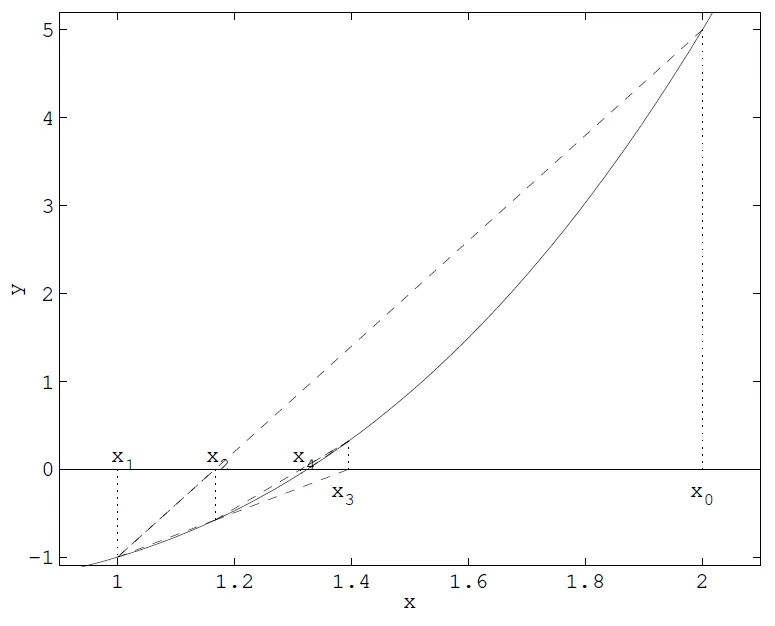

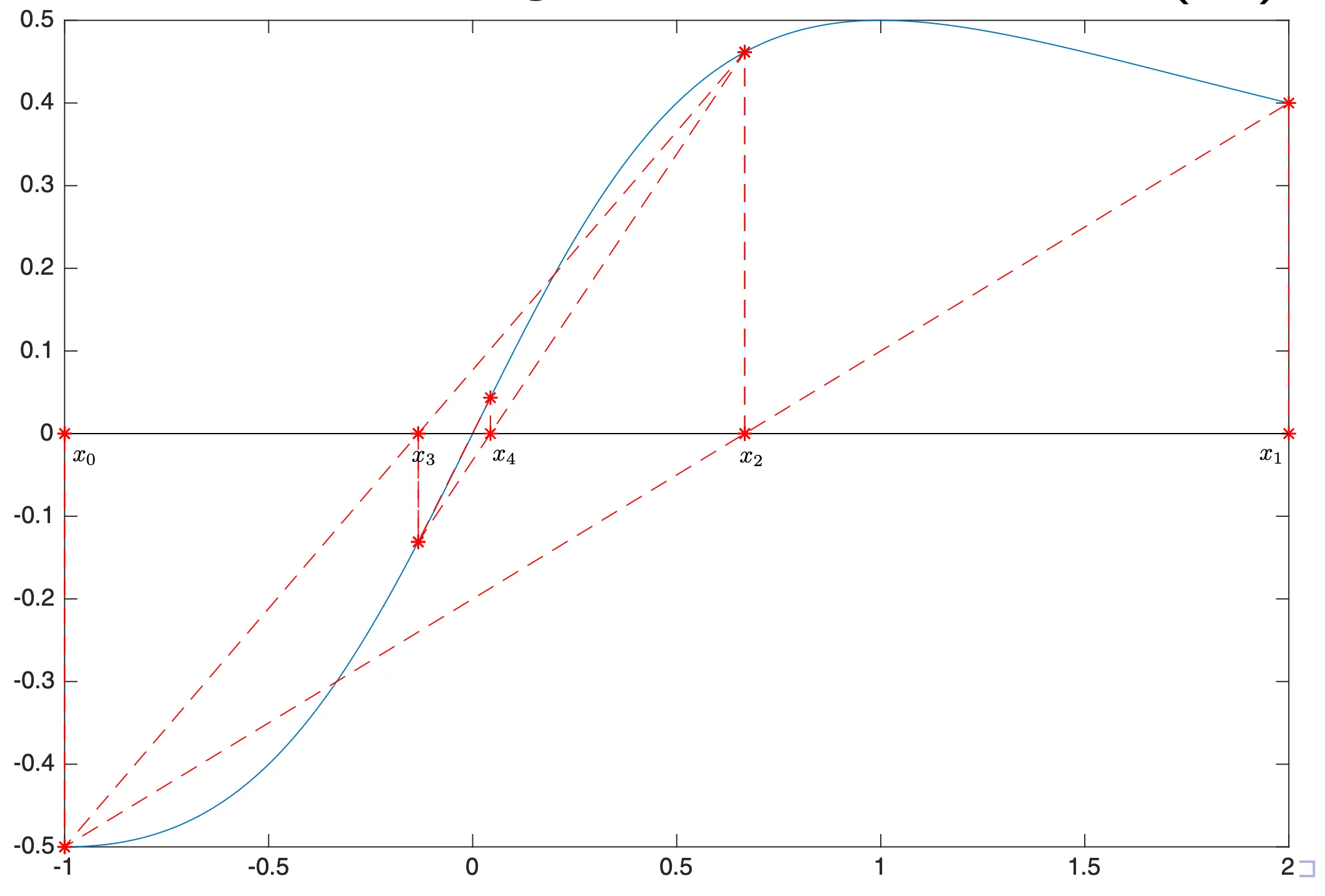
  $$g(x_{k+1}) = x_k - \frac{f(x_k)(x_k - x_{k-1})}{f(x_k) - f(x_{k-1})}$$

  

• Metoda regula falsi
  Je bracketing metoda, tedy metoda, která využívá intervalu, ve kterém se nachází kořen. Nemusí se použít iterativně, ale v iterativní podobě tento interval postupně zmenšuje. ⁸

  $$x_{k+1} = x_k - \frac{x_k - x_s}{f(x_k) - f(x_s)} f(x_k)$$

  kde $s$ je největší index takový, že $f(x_k)f(x_s) < 0$.

  

• Metoda Binary search
  Prvotní interval $(x_0, x_1)$ musí obsahovat kořen funkce $f$, tj. $x_0$ a $x_1$ mají různé znaménka. V každém kroku se rozdělí interval na dvě poloviny a dál hledáme v polovině která obsahuje kořen funkce. Metoda regula falsi se pokouší o rychlejší kovergenci sofistikovanějším dělením intervalu.

Přímé metody pro řešení systému lineárních rovnic

Gaussova eliminace

Systém rovnice je přepsán do matice. Gaussova eliminace je posloupnost operací, jejichž cílem je převést matici do horní trojúhelníkové matice (row echelon form). ⁹ Povoleny jsou následující operace:

• výměna dvou řádků,
• vynásobení řádku nenulovou konstantou,
• přičtení násobku jednoho řádku k jinému.

Jacobiho iterační metoda

Iterativní algoritmus pro řešení soustavy lineárních rovnic. Rozděluje vstupní matici lineárních rovnic na matici diagonál $D$, dolní trojúhelníkovou matici $L$ a horní trojúhelníkovou matici $U$. ¹⁰

Nechť $A\mathbf{x} = \mathbf{b}$ je systém $n$ lineárních rovnic. Tedy:

$$A = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{bmatrix}, \qquad \mathbf{x} = \begin{bmatrix} x_{1} \\ x_2 \\ \vdots \\ x_n \end{bmatrix} , \qquad \mathbf{b} = \begin{bmatrix} b_{1} \\ b_2 \\ \vdots \\ b_n \end{bmatrix}.$$

Algoritmus vypadá takto:

1. Zvolíme počáteční odhad $\mathbf{x}^{(0)}$, nejčastěji $\vec{0}$.

2. Nový odhad získáme ze vztahu:

   $$\mathbf{x}^{(k+1)} = D^{-1}(\mathbf{b} - (L + U)\mathbf{x}^{(k)})$$

Jelikož $L + U = A - D$, dá to zapsat i jako:

$$\mathbf{x}^{(k+1)} = D^{-1}\mathbf{b} + (I - D^{-1} A) \mathbf{x}^{(k)}$$

• Spektrální poloměr
  Spektrální poloměr $\rho$ matice $A$ je největší absolutní hodnota vlastního čísla matice $A$.

  $$\rho(A) = \max_{i=1,\ldots,n} |\lambda_i|$$

• (Řádková) diagonální dominance
  Matice $A$ je diagonálně dominantní, pokud platí:

  $$|a_{ii}| > \sum_{j=1, j \neq i}^n |a_{ij}|$$

  Tedy absolutní hodnota prvku na diagonále je větší než součet absolutních hodnot všech ostatních prvků v řádku.

  • Striktní: nerovnost je ostrá ($>$).
  • Slabá: nerovnost je neostá ($\ge$).

  Analogicky se definuje sloupcová diagonální dominance.

• Konvergence Jacobiho metody
  Jacobiho metoda konveguje pokud všechny následující podmínky:

  1. Nechť $T_j = I - D^{-1} A$ je matice iterace Jacobiho metody. Pak Jacobiho metoda konverguje, pokud:

     $$\rho(T_j) < 1$$

  2. Jacobiho metoda konverguje pro libovolný počáteční odhad $\mathbf{x}^{(0)}$, pokud $A$ je diagonálně dominantní (sloupcově nebo řádkově).

Gaussova-Seidelova iterační metoda

Iterativní metoda pro řešení soustavy lineárních rovnic. Dělí vstupní matici na spodní trojúhelníkovou matici $L_*$ (včetně diagonály, tedy $L_* = D + L$) a striktně horní trojúhelníkovou matici $U$ (diagonála je nulová). Algoritmus vypadá takto: ¹¹

1. Zvolíme počáteční odhad $\mathbf{x}^{(0)}$.

2. Nový odhad získáme ze vztahu:

   $$\mathbf{x}^{(k+1)} = L_*^{-1}(\mathbf{b} - U\mathbf{x}^{(k)}).$$

Alternativně:

$$\begin{aligned} T_{gs} &= (D + L)^{-1} U = L_*^{-1} U \\ \mathbf{x}^{(k+1)} &= T_{gs} \mathbf{x}^{(k)} + g,\quad g = L_*^{-1} \mathbf{b} \end{aligned}$$

• Konvergence Gaussovy-Seidelovy metody
  Analogicky jako u Jacobiho metody, ale místo matice $T_j$ se použije matice $T_{gs} = (D + L)^{-1} U$.

Relaxační iterativní metody

Modifikace Gauss-Seidelovy metody. Využívá parametr $\omega$, který určuje, jak moc se má nový odhad lišit od předchozího. Vztah pro další iteraci se mění na: ¹²

$$\begin{align*} \mathbf{x}^{(k+1)} &= (D - \omega L)^{-1} [(1-\omega)D + \omega U]\mathbf{x}^{(k)} + \omega(D - \omega L)^{-1}\mathbf{b} \\ T_\omega &= (D - \omega L)^{-1} [(1-\omega)D + \omega U] \end{align*}$$

• Pro $0 < \omega < 1$ se názývá metodou dolní relaxace. Je vhodná v případě, kdy Gauss-Seidel nekonverguje.
• Pro $\omega = 1$ je totožná s Gauss-Seidelem.
• Pro $\omega > 1$ se názývá metodou horní relaxace / SOR metodou. Zrychluje konvergenci Gauss-Seidela.

Dekompozice matic

Metody podobné Gaussově eliminaci, ale s vlastnostmi, které mohou být vyhodné.

• LU dekompozice
  Rozdělení matice $A$ na horní dolní trojúhelníkovou matici $L$ a horní trojúhelníkovou matici $U$, tak že $A = LU$.

  Je to v podstatě Gaussova eliminace. Matice $P$ je permutační matice, která prohazuje řádky:

  $$P \cdot A = L \cdot U$$

  Platí, že:

  $$\begin{aligned} A \cdot x &= b \\ A &= LU \\ LU \cdot x &= b \end{aligned}$$

  Původní problém řešení soustavy linárních rovnic se tedy převede na dva problémy:

  $$\begin{aligned} y &= U \cdot x \\ L \cdot y &= b \\ \end{aligned}$$

  Řešíme tedy dva systémy rovnic s trojúhelníkovými maticemi.

  Oproti Gaussovi je výhodnější pro:

  • Opakované řešení soustav s maticí $A$ a různými pravými stranami $b$.
  • Inverzi matice $A$.
  • Výpočet determinantu matice $A$.

• QR dekompozice
  Rozdělení matice $A$ na ortogonální matici $Q$ a horní trojúhelníkovou matici $R$ (už ne $U$), tak že $A = QR$.

  $$\begin{aligned} A \cdot x &= b \\ A = QR \Rightarrow U \cdot x &= Q^T \cdot b \\ \end{aligned}$$

  Protože je ortogonální a tedy $Q^{-1} = Q^T$.

  Má lepší numerickou stabilitu než LU dekompozice.

Numerická diferenciace

Algoritmy numerické diferenciace (derivace) počítají odhady derivace reálných funkcí — aproximují $f'(x)$. Využívají při tom známé hodnoty této funkce a jiné znalosti a předpoklady. ¹³

Numerická diferenciace se využívá pro aproximaci differenciálních rovnic (převodem na diferenční rovnice).

• Langrangeova interpolace
  Pokud známe hodnoty $f$ můžeme mezi nimi interpolovat pomocí Lagrangeova polynomu a derivovat ten, protože derivovat polynomy je jednoduché.

  Important

  Lagrangeovu interpolaci řeší část otázky Křivky a povrchy.

• Finite difference method
  Rodina metod numerické diferenciace, které využívají konečné diference. Tedy approximují limitu v definici derivace malými posuny ve vstupních hodnotách diferenciovaných funkcí. ¹⁴

  Jednotlivým “odstínům” — konkrétním výpočetním vzorcům — téhle metody se říká diferenciační schémata.

  Tip

  Abych pravdu řekl, nepodařilo se mi najít zdroj pro konkrétní definici pojmu “diferenciační schéma”.

• (Konečné) diference prvního řádu / first-order (finite) differences
  Nejjednodušší schéma numerické diferenciace. Vychází z definice derivace. ¹⁵

  • Dopředná diference / forward (finite) difference

    $$\frac{\partial f}{\partial x} \approx \frac{f(x+h) - f(x)}{h}$$

  • Zpětná diference / backward (finite) difference

    $$\frac{\partial f}{\partial x} \approx \frac{f(x) - f(x-h)}{h}$$

  • Centrální diference / central (finite) difference

    $$\frac{\partial f}{\partial x} \approx \frac{f(x+h) - f(x-h)}{2h}$$

  kde $h$ je kladné číslo napodobující nekonečně malou změnu (limitu) v definici derivace. Může to být konstanta, může ale být i zvoleno adaptivně.

  Tip

  Tečna je tak napodobena sečnou.

• Richardson extrapolation
  Způsob zlepšení rate of convergence iterativních metod. ¹⁶

Zdroje

1. Wikipedia: Numerical analysis ↩

2. Wikipedia: Numerical stability ↩

3. Wikipedia: Rate of convergence ↩ ↩²

4. Wikipedia: Numerická metoda ↩

5. What is the intuitive meaning of order of accuracy and order of approximation? ↩

6. Wikipedia: Root-finding algorithms ↩ ↩²

7. MA018 Numerical Methods (podzim 2019) ↩

8. Wikipedia: Regula falsi ↩

9. Wikipedia: Gaussian elimination ↩

10. Wikipedia: Jacobi method ↩

11. Wikipedia: Gauss-Seidel method ↩

12. Wikipedia: Relaxation (iterative method) ↩

13. Wikipedia: Numerical differentiation ↩

14. Wikipedia: Finite difference method ↩

15. Wikipedia: Finite difference ↩

16. Wikipedia: Richardson extrapolation ↩